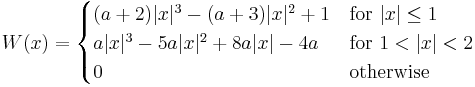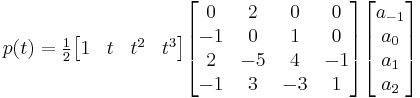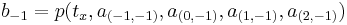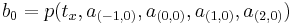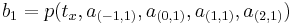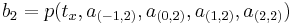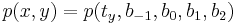Bicubic interpolation
In mathematics, bicubic interpolation is an extension of cubic interpolation for interpolating data points on a two dimensional regular grid. The interpolated surface is smoother than corresponding surfaces obtained by bilinear interpolation or nearest-neighbor interpolation. Bicubic interpolation can be accomplished using either Lagrange polynomials, cubic splines, or cubic convolution algorithm.
In image processing, bicubic interpolation is often chosen over bilinear interpolation or nearest neighbor in image resampling, when speed is not an issue. In contrast to bilinear interpolation, which only takes 4 pixels (2x2) into account, bicubic interpolation also considers the 16 pixels around it (for a total of 4x4 pixels) while computing an average. Images resampled with bicubic interpolation are smoother and have fewer interpolation artifacts.
Contents |
Bicubic interpolation
Suppose the function values  and the derivatives
and the derivatives 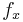 ,
, 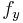 and
and 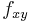 are known at the four corners
are known at the four corners 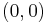 ,
, 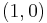 ,
, 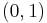 , and
, and 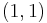 of the unit square. The interpolated surface can then be written
of the unit square. The interpolated surface can then be written
The interpolation problem consists of determining the 16 coefficients 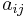 . Matching
. Matching 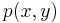 with the function values yields four equations,
with the function values yields four equations,
Likewise, eight equations for the derivatives in the  -direction and the
-direction and the  -direction
-direction
And four equations for the cross derivative 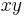 .
.
where the expressions above have used the following identities,
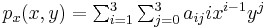
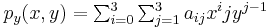
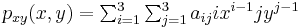 .
.
This procedure yields a surface 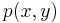 on the unit square
on the unit square ![[0,1] \times [0,1]](/2012-wikipedia_en_all_nopic_01_2012/I/38c7b34812cb087f3562f9ebc984e3c8.png) which is continuous and with continuous derivatives. Bicubic interpolation on an arbitrarily sized regular grid can then be accomplished by patching together such bicubic surfaces, ensuring that the derivatives match on the boundaries.
which is continuous and with continuous derivatives. Bicubic interpolation on an arbitrarily sized regular grid can then be accomplished by patching together such bicubic surfaces, ensuring that the derivatives match on the boundaries.
If the derivatives are unknown, they are typically approximated from the function values at points neighbouring the corners of the unit square, e.g. using finite differences.
Grouping the unknown parameters 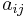 in a vector,
in a vector,
and letting
![x=\left[\begin{smallmatrix}f(0,0)&f(1,0)&f(0,1)&f(1,1)&f_x(0,0)&f_x(1,0)&f_x(0,1)&f_x(1,1)&f_y(0,0)&f_y(1,0)&f_y(0,1)&f_y(1,1)&f_{xy}(0,0)&f_{xy}(1,0)&f_{xy}(0,1)&f_{xy}(1,1)\end{smallmatrix}\right]^T](/2012-wikipedia_en_all_nopic_01_2012/I/9c3e51bfcb0a7ee1d142a2ad577b2fce.png) ,
,
the problem can be reformulated into a linear equation 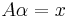 where its inverse is:
where its inverse is:
![A^{-1}=\left[\begin{smallmatrix}
1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
-3 & 3 & 0 & 0 & -2 & -1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
2 & -2 & 0 & 0 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -3 & 3 & 0 & 0 & -2 & -1 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 2 & -2 & 0 & 0 & 1 & 1 & 0 & 0 \\
-3 & 0 & 3 & 0 & 0 & 0 & 0 & 0 & -2 & 0 & -1 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & -3 & 0 & 3 & 0 & 0 & 0 & 0 & 0 & -2 & 0 & -1 & 0 \\
9 & -9 & -9 & 9 & 6 & 3 & -6 & -3 & 6 & -6 & 3 & -3 & 4 & 2 & 2 & 1 \\
-6 & 6 & 6 & -6 & -3 & -3 & 3 & 3 & -4 & 4 & -2 & 2 & -2 & -2 & -1 & -1 \\
2 & 0 & -2 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 2 & 0 & -2 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 1 & 0 \\
-6 & 6 & 6 & -6 & -4 & -2 & 4 & 2 & -3 & 3 & -3 & 3 & -2 & -1 & -2 & -1 \\
4 & -4 & -4 & 4 & 2 & 2 & -2 & -2 & 2 & -2 & 2 & -2 & 1 & 1 & 1 & 1
\end{smallmatrix}\right]](/2012-wikipedia_en_all_nopic_01_2012/I/14242c2a47ab87a56e4a2b592a5410a5.png) .
.
Bicubic convolution algorithm
Bicubic spline interpolation requires the solution of the linear system described above for each grid cell. An interpolator with similar properties can be obtained by applying a convolution with the following kernel in both dimensions:
where  is usually set to -0.5 or -0.75. Note that
is usually set to -0.5 or -0.75. Note that 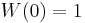 and
and 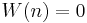 for all nonzero integers
for all nonzero integers  .
.
This approach was proposed by Keys who showed that  (which corresponds to cubic Hermite spline) produces the best approximation of the original function.[1]
(which corresponds to cubic Hermite spline) produces the best approximation of the original function.[1]
If we use the matrix notation for the common case  , we can express the equation in a more friendly manner:
, we can express the equation in a more friendly manner:
for  between 0 and 1 for one dimension. for two dimensions first applied once in
between 0 and 1 for one dimension. for two dimensions first applied once in  and again in
and again in  :
:
Use in computer graphics
The bicubic algorithm is frequently used for scaling images and video for display (see bitmap resampling). It preserves fine detail better than the common bilinear algorithm.
However, due to the negative lobes on the kernel, it causes overshoot (haloing). This can cause clipping, and is an artifact (see also ringing artifacts), but it increases acutance (apparent sharpness), and can be desirable.
See also
- Anti-aliasing
- Bézier surface
- Bilinear interpolation
- Cubic Hermite spline, the one-dimensional analogue of bicubic spline
- Lanczos resampling
- Natural neighbor interpolation
- Sinc filter
- Spline interpolation
- Tricubic interpolation
References
- ^ R. Keys, (1981). "Cubic convolution interpolation for digital image processing". IEEE Transactions on Signal Processing, Acoustics, Speech, and Signal Processing 29 (6): 1153–1160. doi:10.1109/TASSP.1981.1163711.
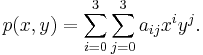
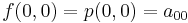
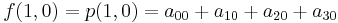
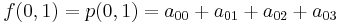
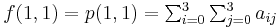
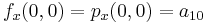
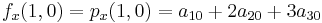
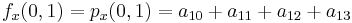
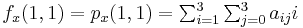
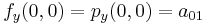
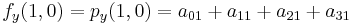
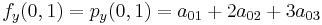
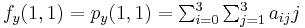
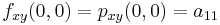
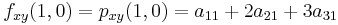
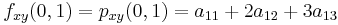
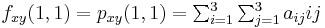
![\alpha=\left[\begin{smallmatrix}a_{00}&a_{10}&a_{20}&a_{30}&a_{01}&a_{11}&a_{21}&a_{31}&a_{02}&a_{12}&a_{22}&a_{32}&a_{03}&a_{13}&a_{23}&a_{33}\end{smallmatrix}\right]^T](/2012-wikipedia_en_all_nopic_01_2012/I/d5e1e201af7911fbc8e9114ecdd3dd7f.png)